M3FNet -- A Radiogenomic Neural Network
A multi-modal fusion model for MGMT enzyme detection
Introduction
Glioblastoma is one of the most common and aggressive forms of brain cancer, with median survival time being only about 14 months. The standard treatments for this disease are surgical resection (where possible) and temozolomide chemotherapy. Temozolomide derives its effectiveness from its ability to methylate the DNA of cancerous cells by attaching an alkyl group on guanine locations, preventing replication and triggering the death of the cell. Unfortunately, some tumor cells are able to fix this type of damage by expressing an enzyme named O-6-methylguanine-DNA methyltransferase (MGMT), a repair enzyme that acts specifically on guanine to remove alkyl groups. Detecting the presence of this biomarker in glioblastoma patients is thus important to cancer management and decision-making.
Detection today is generally dependent on biopsy, and requires a large tissue specimen. Due to glioblastoma’s ability to appear anywhere on the brain, cerebellum and brainstem, it is often difficult to achieve a complete biopsy sample without endangering the patient. Further, it cannot be used for real-time monitoring of methylation status, a current goal of the field. A new area of research termed “radiogenomics” has been proposed to predict the status of MGMT methylation. Radiogenomics seeks to extract genetic information from medical imagery, such as CT scans or MRIs. The founding research in this field used hand-crafted features, involving tumor segmentation, feature extraction, and lengthy manual analysis to identify methylation in patients. Utilizing deep learning to shorten the diagnostic period and improve accuracy has been an emergent force in research, but the difficulty of the task prevents models from attaining particularly high accuracy. My research combines mathematical feature extraction with complicated deep learning models to produce a fuller feature set and more powerful model. Immediate evaluation shows that this model possesses stronger classifying power than most models currently in the field.
The Model and Data
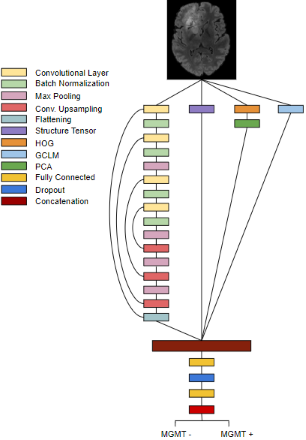
This model is dependent on 4 separate feature extractors – Structure Tensors, Gray-Level Co-Occurrence Matrix (GLCM), Histogram of Gradients (HOG), and a deep learning model. These four extractors are bound into a singular fusion model that is responsible for classifying MGMT presence. The data comes from the 2021 RSNA Brain Tumor challenge dataset (BraTS-2021), a commonly used dataset for radiogenomics research.
Preprocessing
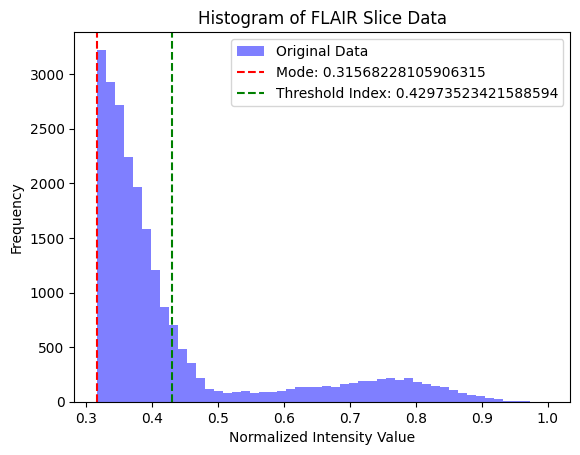
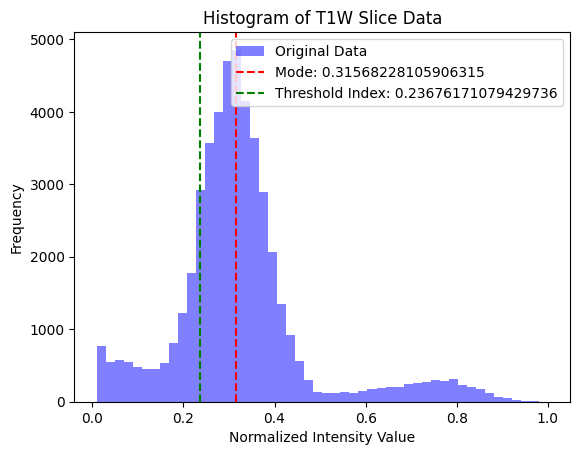
I use two common MRI sequences: Fluid-Attenuated Inversion Recovery (FLAIR) and T1-weighted (T1w) images to derive an initial segmentation of the tumor. T1w images tend to display a darker tumor, and FLAIR images tend to display a lighter tumor. I used a value 20% above and below the mode of the respective image to calculate a rough segmentation of the cancer, then combined those images to get a well-isolated tumor.
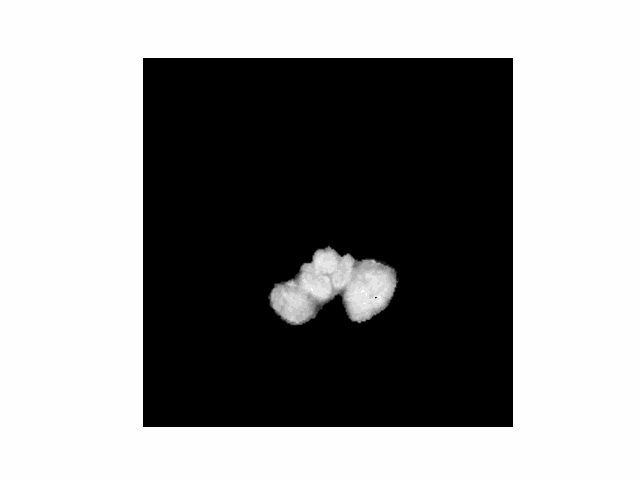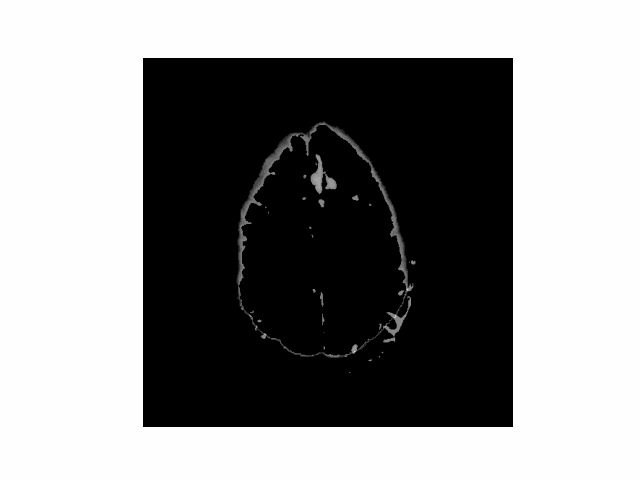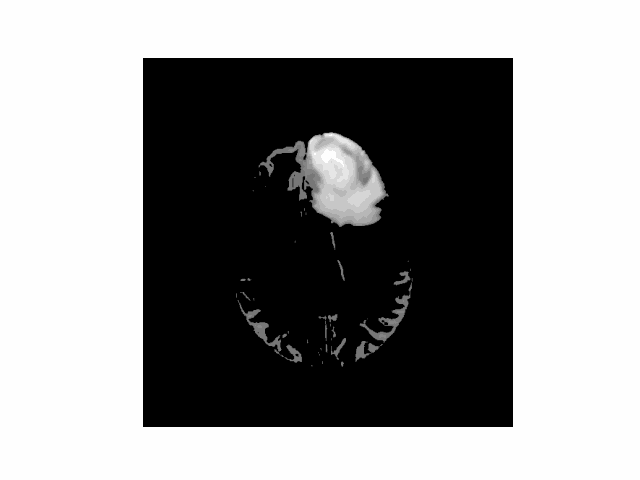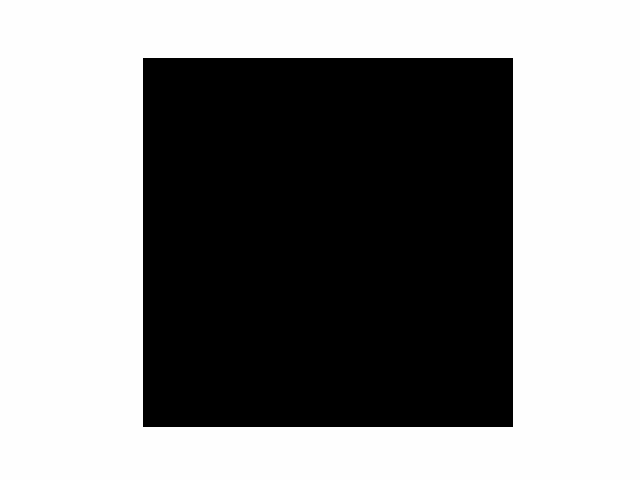
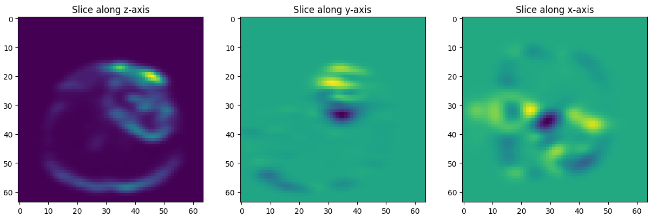
Structure Tensors
Structure tensors are, put simply, matrix representations of partial derivative information. In this instance, it is used to encode local gradient or “edge”. The structure tensor is a matrix of form:
\[S(\mathbf{u})=\begin{pmatrix} [W \ast I_x^2](\mathbf{u}) & [W \ast (I_xI_y)](\mathbf{u})\\ [W \ast (I_xI_y)](\mathbf{u}) & [W \ast I_y^2](\mathbf{u}) \end{pmatrix}\]where \(W\) is a smoothing kernel and \(I_x\) is the gradient in the direction \(x\) (and the same for \(I_y\)), and \(u = (x,y)\), the location where the structure tensor is evaluated. Structure tensors have been used several times as validation for diffusion MRIs (d-MRI), which seek to characterize brain tissue on a microscopic scale. In this model, the structure tensor is used to encode local anisotropic features of tumor microstructures, as well as overall information about the shape and form of the brain. Using structure tensors allows us to average the effects of many cellular structures and get a more clear idea about the orientation and health of nerves and structural brain connections.
HOG
HOG is a feature extractor focused on object detection. It’s similar to SIFT and shape contexts, but uses a overlapping local contrast normalization, which gives us slightly more accuracy in this context. The theory behind HOG is simple: extract the direction and orientation of a gradient that helps describe the structure of the input image. Gradients are calculated by using the Sobel kernel function, then we calculate the magnitude and angle at every pixel using the following mathematical formulation:
\[\left( \begin{array}{c} \|a\| \\ \theta \\ \phi \end{array} \right) = \left( \begin{array}{c} \sqrt{x^2 + y^2 + z^2} \\ tan^-1(\frac{y}{x}) \\ cos^-1(\frac{z}{r} \end{array} \right)\]Finally, these extracted cells are combined into blocks and the histogram of gradients is computed (and is further normalized using L2-norm: \(\frac{v_i}{\sqrt{T_{2}^2 + \epsilon^2}}\), where \(v\) denotes the non-normalized vector.) The features collected from all the normalized blocks are fused to form a feature descriptor for the entire image. This model computes PCA over the feature descriptor to reduce the computational burden.
Model Structure
This model fuses together mathematical and structural features from HOG, GLCM, and the structure tensor. Latent features are extracted using a CNN with recurrent connections to ensure training stability. These feature descriptors and latent information are fused into a single, holistic representation of the most important elements of the input image. Finally, fully connected layers parse this information and return classificationto ensure training stability. These feature descriptors and latent information are fused into a single, holistic representation of the input image. Finally, fully connected layers parse the embedding and feed into a softmax output to determine the presence of MGMT methylation.